이번시간에는 그래프이론(Graph Theory)과 네트워크 분석(Network Analysis)의 주요 개념과 활용사례 등에
대해서 학습해 보자.
1. 그래프 이론(Graph Theory)
1) 기본 개념
그래프 이론은 객체 간의 네트워크 구조와 그들 간의 관계를 분석하며, 정점의 집합과 간선의 집합으로
구성된 그래프를 연구하는 수학의 한 분야로, 정점(노드)들이 엣지(링크)로 연결된 추상적인 표현을 다룹니다.
그래프 이론은 방향 그래프, 비방향 그래프, 가중치 그래프, 비가중치 그래프 등 다양한 종류의
그래프를 분석하기 위한 이론적 틀을 제공하며, 다양한 관계와 연결성을 모델링하는 데 유용합니다.
일상생활의 다양한 문제를 해결하는 데 중요한 도구가 되어 왔으며, 연결성, 순환, 경로, 그래프 색칠과 같은
기본 개념을 이해하는 데 중점을 두며, 종종 실제 시스템과 직접적인 관련 없이 연구되는 경우도 있습니다.
2) 시초
18세기 쾨니히스베르크라는 도시에 있는 두 개의 큰 섬이 총 7개의 다르고 연결되어 있을 때 어떻게 하면
모든 다리를 단 한 번씩만 건너서 다시 원래 위치로 돌아올 수 있을까?라는 질문에 대하여 오일러는
이 문제를 해결하기 위해 그래프라는 개념을 도입하여, 불필요한 요소를 제거하고, 핵심적인 부문만
추상화하여 문제를 단순화시킨 것으로 Graph Theory 의 시작입니다.
섬 A, B는 노드 (vertext, 꼭지점)는 이라 지칭하고, 다리는 엣지 (edge, 간선)으로 지칭합니다.

그래프 이론은 주로 네트워크 통신에서는 라우팅 알고리즘, 최단 경로 도출 등에 사용되며, 사회 네트워크
분석에서는 소셜 네트워크의 구조와 특성을 파악하는 데 사용됩니다.
다시 말씀드리자면, 그래프는 정점(Vertex)과 간선(Edge)으로 구성됩니다.
정점은 개체나 이벤트를 나타내고, 간선은 정점 간의 관계를 나타냅니다. 그래프는 G = (V, E)로 표현되며,
여기서 V는 정점의 집합이고 E는 간선의 집합입니다.
간선은 무방향 간선(양방향), 방향 간선(단방향)으로 나뉠 수 있습니다.
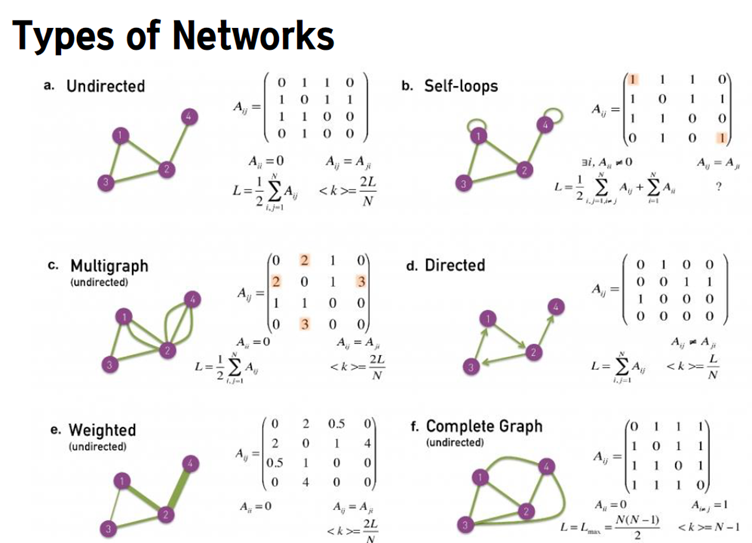
3) 그래프의 종류
아래와 같이 크게 4가지 종류가 있습니다.
- 무방향 그래프: 간선에 방향이 없는 그래프로, 간선은 단순히 정점들의 연결을 나타냅니다.
- 방향 그래프: 간선에 방향이 있는 그래프로, 간선은 정점 간의 방향성 있는 관계를 나타냅니다.
- 가중 그래프: 간선에 가중치가 있는 그래프로, 간선은 연결된 두 정점 간의 가중치를 나타냅니다.
- 다중 그래프: 하나의 정점 쌍 사이에 여러 개의 간선이 존재할 수 있는 그래프입니다
4) 그래프 이론에서의 주요 용어
- 경로(Path): 두 정점 사이를 연결하는 간선들의 순서 된 집합입니다.
- 사이클(Cycle): 한 정점에서 시작하여 다시 돌아와 자기 자신을 포함하는 경로입니다.
- 연결성(Connectivity): 그래프 내에서 정점들이 서로 연결되어 있는 정도를 나타냅니다.
- 차수(Degree): 각 정점에 연결된 간선의 수를 나타냅니다.
- 정점(Vertex): 그래프에서 개별적인 노드.
- 간선(Edge): 정점 간의 연결을 나타냄.
- 가중치(Weight): 간선에 부여된 값 (예: 거리, 비용).
- 인접 행렬(Adjacency Matrix): 그래프를 행렬로 표현.
- 인접 리스트(Adjacency List): 정점과 간선의 관계를 리스트로 표현.
5) 그래프 알고리즘과 응용
그래프 이론은 다양한 분야에서 네트워크의 구조와 관계를 분석하는 데에 활용되며, 이를 통해 복잡한 현상을
이해하고 해결하는 데에 중요한 역할을 합니다.
또한, 그래프 이론은 다양한 알고리즘과 응용을 통해 실제 문제에 대한 해결책을 제공하고 있습니다.
알고리즘에서는 다익스트라 알고리즘, 벨만-포드 알고리즘 등의 그래프 알고리즘이 널리 사용됩니다.
2. 네트워크 분석(Network Analysis)
1) 주요 개념
네트워크 과학은 그래프 이론의 원리를 적용하여 실제 시스템에서 발견되는 복잡한 네트워크를 연구하는
분야입니다. 기술적 네트워크, 컴퓨터 과학, 사회학 네트워크 등 다양한 학문 분야, 다양한 네트워크 구조를
분석하여 중요한 노드나 패턴을 발견하고, 여러 도메인에서 관찰되는 실제 문제와 현상을 다룹니다.
네트워크 과학의 목표는 이러한 네트워크의 구조, 동역학 및 기능을 이해하는 것이며, 종종 경험적 데이터를
통합하고 노드와 엣지의 속성을 고려합니다.
중요한 개념으로는 중심성(Centrality), 군집화(Clustering), 전염병 확산 모델 등이 있습니다.
네트워크 분석은 사회적 연결성을 이해하고, 운송 및 라우팅 문제는 효율적인 자원 할당을 돕고,
컴퓨터 네트워크는 효율적인 네트워크 구조를 설계하는 데에 활용됩니다.
또한, 알고리즘과 최적화 문제에서는 그래프 이론이 최적의 해결책을 찾는 데에 중요한 도구로 활용됩니다.

2) 활용 분야
네트워크 분석 분야는 다양한 학문 분야 중 '네트워크'라는 하나의 주제로 통일되면서 발생한 학제 간 연구 분야
복잡계 네트워크 (Complex Network)로써 사회 현상의 탐구측면에서는 소셜 네트워크 등의 사람과 사람
사이의 관계 분석과 생명 현상의 탐구 측면에서 인체 단백질 네트워크 (분자와 분자 사이의 관계 분석) 및
자연 현상의 탐구 (상전이 현상 - 네트워크 동역학으로 분석 가능) 등입니다.
3) 실제 응용 사례
- 금융 사기 탐지(거래 네트워크를 분석해 이상 거래 탐지)
- 교통 네트워크 분석 (최적의 경로 찾기 및 교통 흐름 관리) 등
4) 네트워크 구조
노드(엔티티)와 엣지(연결)가 어떻게 조직되는지를 의미하며, 주요 네트워크 구조 유형에는 랜덤 네트워크,
스몰월드 네트워크, 스케일-프리 네트워크, 모듈형 네트워크가 있습니다.
- 랜덤 네트워크는 임의로 형성된 연결을 나타냅니다. 1960년에 도입된 Erdős-Rényi (ER) 랜덤 네트워크
모델은 랜덤 그래프를 연구하는 기본적인 틀입니다.
이 모델에서 그래프는 𝑁개의 노드로 구성되며, 각 노드 쌍은 확률 𝑝로 연결됩니다.
그래프는 𝑁(노드의 수)과 𝑝(연결 확률)에 의해 파라미터화됩니다. - 스몰월드 네트워크는 지역적 군집과 짧은 경로를 가진 밀접한 관계를 강조하며, 6단계만 걸치면
세상 대부분의 사람과 연락할 수 있으므로, 세상이 참 좁은 이유에 대한 과학적 설명해 주게 됩니다. - 스케일-프리 네트워크는 높은 연결성을 가진 허브를 강조하고,
- 모듈형 네트워크는 뚜렷한 커뮤니티를 가진 모듈화 된 구조를 보여줍니다.